Page 794 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

770 MÉTODOS RÍGIDOS Y DE PASOS MÚLTIPLES

y
1.5 h = 0.0015

1

Exacto
0.5
h = 0.0005
0
0 0.002 0.004 0.006 t
a)
y
2

Exacto

1

h = 0.05

0
0 0.1 0.2 0.3 0.4 t
b)

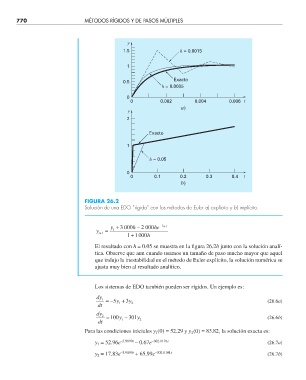
FIGURA 26.2
Solución de una EDO “rígida” con los métodos de Euler a) explícito y b) implícito.

− t i+1
h − 2 000
he
y + 3 000
y i+1 = i
1 +1 000 h
El resultado con h = 0.05 se muestra en la fi gura 26.2b junto con la solución analí-
tica. Observe que aun cuando usamos un tamaño de paso mucho mayor que aquel
que indujo la inestabilidad en el método de Euler explícito, la solución numérica se
ajusta muy bien al resultado analítico.

Los sistemas de EDO también pueden ser rígidos. Un ejemplo es:
dy
1 =− y 5 + y 3 (26.6a)
dt 1 2
dy
2 = 100 y − 301 y (26.6b)
dt 1 2
Para las condiciones iniciales y (0) = 52.29 y y (0) = 83.82, la solución exacta es:
1
2
y = 52.96e –3.9899t – 0.67e –302.0101t (26.7a)
1
y 2 = 17.83e –3.9899t + 65.99e –302.0101t (26.7b)

6/12/06 14:02:31
Chapra-26.indd 770
Chapra-26.indd 770 6/12/06 14:02:31