Page 797 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

26.2 MÉTODOS DE PASOS MÚLTIPLES 773

0
y Pendiente = f (x , y )
i+1
i–1

x i–1
x i x i+1 x

a)
0
f (x , y )+ f (x , y )
y Pendiente = i i i+1 i–1
2

x i x i+1 x

b)

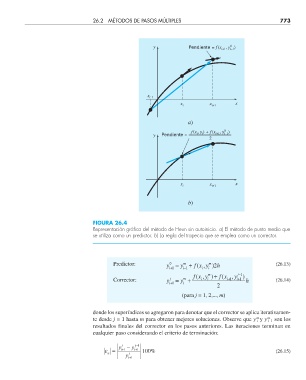
FIGURA 26.4
Representación gráfi ca del método de Heun sin autoinicio. a) El método de punto medio que
se utiliza como un predictor. b) La regla del trapecio que se emplea como un corrector.

m
0
Predictor: y = y + f x y 2(, m ) h (26.13)
i+1 i−1 i i
j−1
m
(,
i
m
j
i
Corrector: y = y + fx y ) + fx ( i+1 y , i+1 ) h (26.14)
i+1
i
2
(para j = 1, 2,..., m)
donde los superíndices se agregaron para denotar que el corrector se aplica iterativamen-
m
m
te desde j = 1 hasta m para obtener mejores soluciones. Observe que y i y y i–1 son los
resultados finales del corrector en los pasos anteriores. Las iteraciones terminan en
cualquier paso considerando el criterio de terminación:
j
j−1
ε = y i+1 − y i+1 100% (26.15)
a
y j
i+1
6/12/06 14:02:32
Chapra-26.indd 773
Chapra-26.indd 773 6/12/06 14:02:32