Page 805 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

26.2 MÉTODOS DE PASOS MÚLTIPLES 781

y

Interpolación

x
a)
y

x
b)
y

x
c)

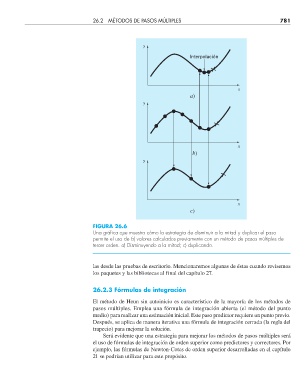
FIGURA 26.6
Una gráfi ca que muestra cómo la estrategia de disminuir a la mitad y duplicar el paso
permite el uso de b) valores calculados previamente con un método de pasos múltiples de
tercer orden. a) Disminuyendo a la mitad; c) duplicando.

las desde las pruebas de escritorio. Mencionaremos algunas de éstas cuando revisemos
los paquetes y las bibliotecas al final del capítulo 27.

26.2.3 Fórmulas de integración
El método de Heun sin autoinicio es característico de la mayoría de los métodos de
pasos múltiples. Emplea una fórmula de integración abierta (el método del punto
medio) para realizar una estimación inicial. Este paso predictor requiere un punto previo.
Después, se aplica de manera iterativa una fórmula de integración cerrada (la regla del
trapecio) para mejorar la solución.
Será evidente que una estrategia para mejorar los métodos de pasos múltiples será
el uso de fórmulas de integración de orden superior como predictores y correctores. Por
ejemplo, las fórmulas de Newton-Cotes de orden superior desarrolladas en el capítulo
21 se podrían utilizar para este propósito.

6/12/06 14:02:35
Chapra-26.indd 781 6/12/06 14:02:35
Chapra-26.indd 781