Page 810 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

786 MÉTODOS RÍGIDOS Y DE PASOS MÚLTIPLES

y

x x x x x x
i –3 i –2 i –1 i i +1
a)
y

x i –2 x i –1 x i x i +1 x
b)

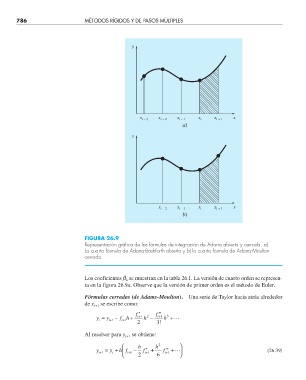
FIGURA 26.9
Representación gráfi ca de las fórmulas de integración de Adams abierta y cerrada. a)
La cuarta fórmula de Adams-Bashforth abierta y b) la cuarta fórmula de Adams-Moulton
cerrada.

Los coeficientes b se muestran en la tabla 26.1. La versión de cuarto orden se represen-
k
ta en la figura 26.9a. Observe que la versión de primer orden es el método de Euler.
Fórmulas cerradas (de Adams-Moulton). Una serie de Taylor hacia atrás alrededor
de x se escribe como:
i+1
f ′ f ′′
y = y i+1 − f h + i+1 h − 3! h +
3
2
i+1
2
i+1
i
Al resolver para y se obtiene:
i+1
⎛ h h 2 ⎞
⎜
y = y + h f − f ′ + f ′′ + ⎟ (26.39)
i+1 i ⎝ i+1 2 i+1 6 i+1 ⎠

6/12/06 14:02:36
Chapra-26.indd 786 6/12/06 14:02:36
Chapra-26.indd 786