Page 815 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

26.2 MÉTODOS DE PASOS MÚLTIPLES 791

y

0.005

Método de Milne
Solución verdadera

0
5 10 x

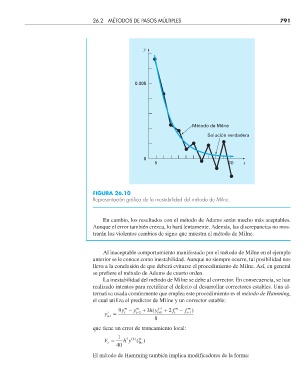
FIGURA 26.10
Representación gráfi ca de la inestabilidad del método de Milne.

En cambio, los resultados con el método de Adams serán mucho más aceptables.
Aunque el error también crezca, lo hará lentamente. Además, las discrepancias no mos-
trarán los violentos cambios de signo que muestra el método de Milne.

Al inaceptable comportamiento manifestado por el método de Milne en el ejemplo
anterior se le conoce como inestabilidad. Aunque no siempre ocurre, tal posibilidad nos
lleva a la conclusión de que deberá evitarse el procedimiento de Milne. Así, en general
se prefiere el método de Adams de cuarto orden.
La inestabilidad del método de Milne se debe al corrector. En consecuencia, se han
realizado intentos para rectificar el defecto al desarrollar correctores estables. Una al-
ternativa usada comúnmente que emplea este procedimiento es el método de Hamming,
el cual utiliza el predictor de Milne y un corrector estable:
m
m
m
j−1
i−2
i
i−1
i
j
y i+1 = 9 y − y m + 3 h y ( i+1 + 2 f − f )
8
que tiene un error de truncamiento local:
E = 1 h y ()ξ
5 ()
4
c c
40
El método de Hamming también implica modificadores de la forma:
6/12/06 14:02:38
Chapra-26.indd 791 6/12/06 14:02:38
Chapra-26.indd 791