Page 823 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat
P. 823
27.1 MÉTODOS GENERALES PARA PROBLEMAS DE VALORES EN LA FRONTERA 799
T, C
200
Lineal
100
No lineal
0
0 5 10 z
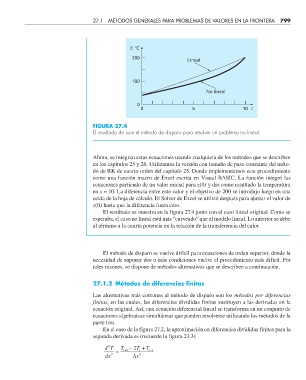
FIGURA 27.4
El resultado de usar el método de disparo para resolver un problema no lineal.
Ahora, se integran estas ecuaciones usando cualquiera de los métodos que se describen
en los capítulos 25 y 26. Utilizamos la versión con tamaño de paso constante del méto-
do de RK de cuarto orden del capítulo 25. Donde implementamos este procedimiento
como una función macro de Excel escrita en Visual BASIC. La función integró las
ecuaciones partiendo de un valor inicial para z(0) y dio como resultado la temperatura
en x = 10. La diferencia entre este valor y el objetivo de 200 se introdujo luego en una
celda de la hoja de cálculo. El Solver de Excel se utilizó después para ajustar el valor de
z(0) hasta que la diferencia fuera cero.
El resultado se muestra en la figura 27.4 junto con el caso lineal original. Como se
esperaba, el caso no lineal está más “curveado” que el modelo lineal. Lo anterior se debe
al término a la cuarta potencia en la relación de la transferencia del calor.
El método de disparo se vuelve difícil para ecuaciones de orden superior, donde la
necesidad de suponer dos o más condiciones vuelve el procedimiento más difícil. Por
tales razones, se dispone de métodos alternativos que se describen a continuación.
27.1.2 Métodos de diferencias fi nitas
Las alternativas más comunes al método de disparo son los métodos por diferencias
finitas, en las cuales, las diferencias divididas finitas sustituyen a las derivadas en la
ecuación original. Así, una ecuación diferencial lineal se transforma en un conjunto de
ecuaciones algebraicas simultáneas que pueden resolverse utilizando los métodos de la
parte tres.
En el caso de la figura 27.2, la aproximación en diferencias divididas finitas para la
segunda derivada es (recuerde la figura 23.3)
2
dT = T − 2 T + T i 1
−
+
i 1
i
dx 2 ∆ x 2
6/12/06 14:03:03
Chapra-27.indd 799 6/12/06 14:03:03
Chapra-27.indd 799