Page 830 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

806 PROBLEMAS DE VALORES EN LA FRONTERA Y DE VALORES PROPIOS

donde A y B son las constantes esenciales y arbitrarias de la integración que serán eva-
luadas por medio de las condiciones de frontera. De acuerdo con la primera condición
[ecuación (27.13a)],

0 = A sen(0) + B cos(0)

Por lo tanto, concluimos que B = 0.
De acuerdo con la segunda condición [ecuación (27.13b)],

0 = A sen(pL) + B cos(pL)

Pero, puesto que B = 0, entonces, A sen(pL) = 0. Como A = 0 representa una solución
trivial, concluimos que sen(pL) = 0. Para que esta igualdad se cumpla,
pL = np para n = 1, 2, 3,… (27.15)

Así, existe un número infinito de valores que satisfacen las condiciones de frontera. De
la ecuación (27.15) se despeja
nπ
P = para n = 1 2 3,, ,… (27.16)
L

los cuales son los valores propios para la columna.
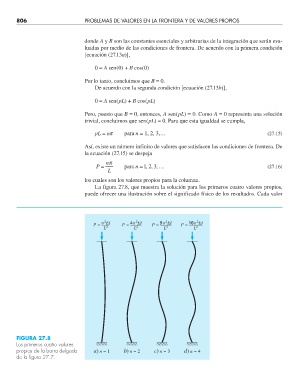
La figura 27.8, que muestra la solución para los primeros cuatro valores propios,
puede ofrecer una ilustración sobre el significado físico de los resultados. Cada valor

2
2
2
2
EI 4 EI 9 EI 16 EI
P = P = P = P =
L 2 L 2 L 2 L 2

FIGURA 27.8
Los primeros cuatro valores
propios de la barra delgada a) n =1 b) n =2 c) n =3 d) n =4
de la fi gura 27.7.

6/12/06 14:03:06
Chapra-27.indd 806
Chapra-27.indd 806 6/12/06 14:03:06