Page 868 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

844 ESTUDIO DE CASOS: ECUACIONES DIFERENCIALES ORDINARIAS

d
dt
0.8
2

0 0
t t
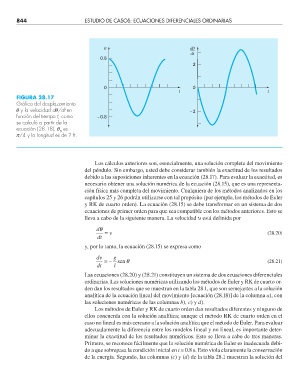
FIGURA 28.17
Gráfi ca del desplazamiento
q y la velocidad dq/dt en –2
función del tiempo t, como –0.8
se calculó a partir de la
ecuación (28.18). q es
0
p/4 y la longitud es de 2 ft.

Los cálculos anteriores son, esencialmente, una solución completa del movimiento
del péndulo. Sin embargo, usted debe considerar también la exactitud de los resultados
debido a las suposiciones inherentes en la ecuación (28.17). Para evaluar la exactitud, es
necesario obtener una solución numérica de la ecuación (28.15), que es una representa-
ción física más completa del movimiento. Cualquiera de los métodos analizados en los
capítulos 25 y 26 podrán utilizarse con tal propósito (por ejemplo, los métodos de Euler
y RK de cuarto orden). La ecuación (28.15) se debe transformar en un sistema de dos
ecuaciones de primer orden para que sea compatible con los métodos anteriores. Esto se
lleva a cabo de la siguiente manera. La velocidad υ está definida por
dθ
= v (28.20)
dt
y, por lo tanto, la ecuación (28.15) se expresa como

dv g
=− sen θ (28.21)
dt l
Las ecuaciones (28.20) y (28.21) constituyen un sistema de dos ecuaciones diferenciales
ordinarias. Las soluciones numéricas utilizando los métodos de Euler y RK de cuarto or-
den dan los resultados que se muestran en la tabla 28.1, que son semejantes a la solución
analítica de la ecuación lineal del movimiento [ecuación (28.18)] de la columna a), con
las soluciones numéricas de las columnas b), c) y d).
Los métodos de Euler y RK de cuarto orden dan resultados diferentes y ninguno de
ellos concuerda con la solución analítica; aunque el método RK de cuarto orden en el
caso no lineal es más cercano a la solución analítica que el método de Euler. Para evaluar
adecuadamente la diferencia entre los modelos lineal y no lineal, es importante deter-
minar la exactitud de los resultados numéricos. Esto se lleva a cabo de tres maneras.
Primero, se reconoce fácilmente que la solución numérica de Euler es inadecuada debi-
do a que sobrepasa la condición inicial en t = 0.8 s. Esto viola claramente la conservación
de la energía. Segundo, las columnas (c) y (d) de la tabla 28.1 muestran la solución del

6/12/06 14:03:41
Chapra-28.indd 844 6/12/06 14:03:41
Chapra-28.indd 844