Page 869 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

28.4 EL PÉNDULO OSCILANTE 845

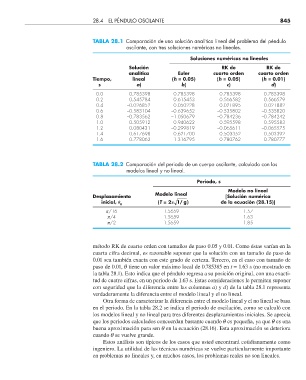
TABLA 28.1 Comparación de una solución analítica lineal del problema del péndulo
oscilante, con tres soluciones numéricas no lineales.
Soluciones numéricas no lineales
Solución RK de RK de
analítica Euler cuarto orden cuarto orden
Tiempo, lineal (h = 0.05) (h = 0.05) (h = 0.01)
s a) b) c) d)
0.0 0.785398 0.785398 0.785398 0.785398
0.2 0.545784 0.615453 0.566582 0.566579
0.4 –0.026852 0.050228 0.021895 0.021882
0.6 –0.583104 –0.639652 –0.535802 –0.535820
0.8 –0.783562 –1.050679 –0.784236 –0.784242
1.0 –0.505912 –0.940622 –0.595598 –0.595583
1.2 0.080431 –0.299819 –0.065611 –0.065575
1.4 0.617698 0.621700 0.503352 0.503392
1.6 0.778062 1.316795 0.780762 0.780777

TABLA 28.2 Comparación del periodo de un cuerpo oscilante, calculado con los
modelos lineal y no lineal.

Periodo, s
Modelo no lineal
Desplazamiento Modelo lineal [Solución numérica
1/
inicial, θ (T = 2π g) de la ecuación (28.15)]
0
p/16 1.5659 1.57
p/4 1.5659 1.63
p/2 1.5659 1.85

método RK de cuarto orden con tamaños de paso 0.05 y 0.01. Como éstas varían en la
cuarta cifra decimal, es razonable suponer que la solución con un tamaño de paso de
0.01 sea también exacta con este grado de certeza. Tercero, en el caso con tamaño de
paso de 0.01, q tiene un valor máximo local de 0.785385 en t = 1.63 s (no mostrado en
la tabla 28.1). Esto indica que el péndulo regresa a su posición original, con una exacti-
tud de cuatro cifras, en un periodo de 1.63 s. Estas consideraciones le permiten suponer
con seguridad que la diferencia entre las columnas a) y d) de la tabla 28.1 representa
verdaderamente la diferencia entre el modelo lineal y el no lineal.
Otra forma de caracterizar la diferencia entre el modelo lineal y el no lineal se basa
en el periodo. En la tabla 28.2 se indica el periodo de oscilación, como se calculó con
los modelos lineal y no lineal para tres diferentes desplazamientos iniciales. Se aprecia
que los periodos calculados concuerdan bastante cuando q es pequeña, ya que q es una
buena aproximación para sen q en la ecuación (28.16). Esta aproximación se deteriora
cuando q se vuelve grande.
Estos análisis son típicos de los casos que usted encontrará cotidianamente como
ingeniero. La utilidad de las técnicas numéricas se vuelve particularmente importante
en problemas no lineales y, en muchos casos, los problemas reales no son lineales.

6/12/06 14:03:41
Chapra-28.indd 845 6/12/06 14:03:41
Chapra-28.indd 845