Page 873 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

PROBLEMAS 849

de estado-espacio. Para este caso, así como para el inciso do numérico. Se aplican los valores siguientes de parámetro:
4
d), use los coeficientes que siguen: a = 0.3, b = 0.01111, c E = 30 000 ksi, I = 800 in , P = 1 kip, L = 10 ft. Compare sus
= 0.2106, d = 0.0002632. resultados numéricos con la solución analítica,
d) Suponga que en 1993, algunos cazadores furtivos incur- PLx 2 Px 3
sionaron en la isla y mataron al 50% de los alces. Prediga y =− +
2 EI 6 EI
cómo evolucionaría la población tanto de lobos como de
28.23 La ecuación diferencial básica de la curva elástica para una
alces hacia el año 2020. Presente sus resultados en gráficas
viga con carga uniforme (véase la figura P28.23) está dada por
tanto de series de tiempo como de estado-espacio.
2
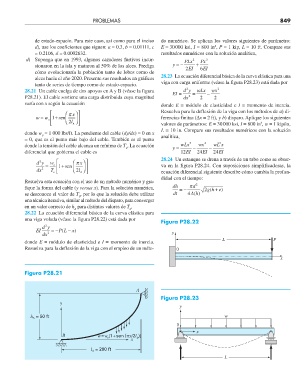
28.21 Un cable cuelga de dos apoyos en A y B (véase la figura EI = dy = wLx − wx 2
P28.21). El cable sostiene una carga distribuida cuya magnitud dx 2 2 2
varía con x según la ecuación donde E = módulo de elasticidad e I = momento de inercia.
⎡ ⎛ π x ⎞ ⎤ Resuelva para la deflexión de la viga con los métodos de a) di-
+
w = w ⎢1 sen ⎜ ⎟ ⎥ ferencias finitas (∆x = 2 ft), y b) disparo. Aplique los siguientes
o
⎣ ⎢ ⎝ 2 l ⎠ ⎥ valores de parámetros: E = 30 000 ksi, I = 800 in , w = 1 kip/in,
A ⎦
4
L = 10 in. Compare sus resultados numéricos con la solución
donde w = 1 000 lbs/ft. La pendiente del cable (dy/dx) = 0 en x
0 analítica,
= 0, que es el punto más bajo del cable. También es el punto
3
donde la tensión del cable alcanza un mínimo de T . La ecuación y = wLx 3 − wx 4 − wL x
0
diferencial que gobierna el cable es 12 EI 24 EI 24 EI
2
dy = w ⎡ ⎢ 1+ sen ⎛ π x ⎞ ⎤ 28.24 Un estanque se drena a través de un tubo como se obser-
va en la figura P28.24. Con suposiciones simplificadoras, la
o
⎜
⎟ ⎥
o ⎣
dx 2 T ⎢ ⎝ l 2 ⎠ ⎥ ecuación diferencial siguiente describe cómo cambia la profun-
A ⎦
didad con el tiempo:
Resuelva esta ecuación con el uso de un método numérico y gra- 2
fique la forma del cable (y versus x). Para la solución numérica, dh =− π d 2 (
gh e+ )
se desconoce el valor de T , por lo que la solución debe utilizar dt 4 Ah ()
0
una técnica iterativa, similar al método del disparo, para converger
en un valor correcto de h para distintos valores de T .
A 0
28.22 La ecuación diferencial básica de la curva elástica para
una viga volada (véase la figura P28.22) está dada por
Figura P28.22
2
dy
EI =− PL −( x) y
dx 2
L P
donde E = módulo de elasticidad e I = momento de inercia.
Resuelva para la deflexión de la viga con el empleo de un méto- 0
x
Figura P28.21
A
Figura P28.23
y
y
h = 50 ft w
A
0
x
B w = w [1 + sen (x/2l )]
o
x a
l = 200 ft
A
L
Chapra-28.indd 849
6/12/06 14:03:43
Chapra-28.indd 849 6/12/06 14:03:43