Page 11 - E-MODUL_MEKANIKA_ANALITIK

g PERSAMAANEULER-LAGRANGE g
PERSAMAANEULER-LAGRANGE

Pada pertemuan sebelumnya, kita telah mempelajari mengenai studi kasus terhadap
permasalahan bagaimana menentukan lintasan terpendek pada sebuah koordinat dan
Prinsip Fermat (Fermat’s Principle). Dari permasalahan tersebut, kita dapat
mengilustrasikan permasalahan tersebut ke dalam bentuk umum (variational
problem),sebagai berikut :

x 2
S = f y x , y' x , x dx (1)
x 1

Dimana y(x) merupakan sebuah kurva yang belum diketahui, yang melalui dua buah
titik (x1,y1) menuju (x2,y2), sehingga y(x1)= y1 dan y(x2)= y2. Perlu diketahui bahwa fungsi f
diatas merupakan fungsi terhadap 3 variabel f = f y, y', x , akan tetapi, karena intergral
melalui lintasan y=y(x) sehingga fungsi f menjadi seperti persamaan di atas.

Studi Kasus #2________________

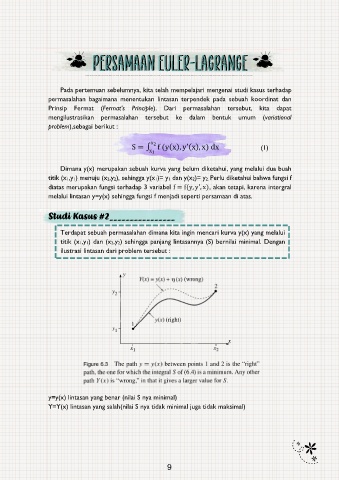
Terdapat sebuah permasalahan dimana kita ingin mencari kurva y(x) yang melalui
titik (x1,y1) dan (x2,y2) sehingga panjang lintasannya (S) bernilai minimal. Dengan
ilustrasi lintasan dari problem tersebut :

y=y(x) lintasan yang benar (nilai S nya minimal)
Y=Y(x) lintasan yang salah(nilai S nya tidak minimal juga tidak maksimal)

u

9